3D bin packing (trodimenzijsko pakiranje) pomoću genetskog algoritma

TLDR

• Implementirao sam rješenje za trodimenzijsko pakiranje s mogućnošću ortogonalnih rotacija objekata i različitih spremnika.
• Rješenje je kombinacija genetskog algoritma (pretraživanje prostora) i heuristike pakiranja temeljene na Empty Maximal Spaces (EMS).
• Kromosom kodira: redoslijed pakiranja (BPS), orijentacije (VBO) i redoslijed odabira spremnika (CLS).
• Kao najbolja heuristika odabira slobodnog prostora pokazala se DFTRC-2, a od operatora križanja one-point crossover (SBX/uniform nisu bili prikladni).
• Usporedio sam heuristike pakiranja i stope mutacije.

Motivacija

Problem pakiranja se u literaturi pojavljuje već od 1970-ih, prvo u 1D i 2D oblicima. Rani pristupi su bili jednostavne heuristike poput First-Fit i Best-Fit, dok se s rastom računalnih mogućnosti sve više prelazi na metaheuristička rješenja (posebno od 90-ih do danas). Praktične primjene su brojne: logistika, skladištenje, planiranje transporta, proizvodnja i općenito svaki sustav gdje želimo minimizirati broj spremnika ili maksimizirati iskorištenje volumena. Ovaj problem je NP-težak, pa se u praksi često koriste aproksimacijski i heuristički pristupi. Posebno mi je zanimljivo što je problem vrlo prisutan u industriji dugo vremena, ali se i dalje aktivno istražuje zbog svoje složenosti i praktične važnosti. U ovom radu fokus je na 3D varijanti uz realistične detalje poput rotacija i nehomogene spremnike.

Problem

Imamo konačni skup objekata, gdje je svaki objekt i definiran dimenzijama (wᵢ, hᵢ, dᵢ). Svaki spremnik b ima dimenzije (Wᵦ, Hᵦ, Dᵦ). Cilj je svakom objektu dodijeliti spremnik i poziciju (te eventualno rotaciju) tako da:

• se objekti ne preklapaju,
• svaki objekt stane u odabrani spremnik,
• i da ukupno koristimo što manje spremnika (ili ekvivalentno: minimiziramo neiskorišten volumen).

Objekte je moguće ortogonalno rotirati, što je ekvivalentno permutaciji dimenzija, pa svaki objekt ima do 6 konfiguracija.

Pristup

Rješenje se sastoji od dvije komponente:

1. Genetski algoritam (GA) koji pretražuje prostor rješenja (redoslijedi i orijentacije).
2. Heuristika pakiranja koja za zadani kromosom pokušava izgraditi konkretan raspored u spremnicima i vraća koliko je spremnika potrebno.

U svakoj iteraciji GA:

• evaluira jedinke pomoću heuristike pakiranja,
• provede selekciju,
• napravi križanje i mutacije,
• te nastavi kroz generacije.

Kodiranje rješenja (kromosom)

Kromosom jedinke je vektor duljine 2n + m:

• prvih n realnih vrijednosti u [0,1] kodira BPS (redoslijed pakiranja objekata),
• drugih n vrijednosti kodira VBO (orijentacije/rotacije objekata),
• zadnjih m vrijednosti kodira CLS (redoslijed odabira spremnika), relevantno ako spremnici nisu homogeni.

Zašto realni brojevi u [0,1]?

• omogućuju jednostavne mutacije i križanja,
• a redoslijed se dobije tako da se objekti sortiraju po pripadnoj vrijednosti.

Rotacije se ne kodiraju direktno kao {0..5}, nego kao koeficijent koji se kasnije mapira na jednu od dozvoljenih rotacija u trenutnom kontekstu spremnika.

Heuristika pakiranja

Empty Maximal Spaces (EMS)

Slobodni prostor u spremniku prikazujem pomoću liste EMS volumena: svaki EMS predstavlja najveći pravokutni prazni blok koji trenutno postoji u spremniku. Nakon svakog smještanja objekta lista EMS-ova se ažurira:

1. odabere se EMS u koji objekt stane,
2. generiraju se novi EMS-ovi na temelju presjeka objekta i odabranog EMS-a,
3. uklone se degenerirani ili redundantni EMS-ovi,
4. opcionalno se uklone EMS-ovi u koje ne stane nijedan preostali objekt.

U praksi se objekt pozicionira u stražnji donji lijevi kut odabranog EMS-a, što ograničava eksploziju broja novih EMS-ova i drži prostor što kompaktnijim.

Heuristike odabira EMS-a

Implementirao sam i usporedio više heuristika:

• First-Fit: uzmi prvi EMS u koji objekt stane.
• Best-Fit: uzmi najmanji EMS u koji objekt stane.
• DFTRC-2: odaberi EMS tako da objekt (u nekoj rotaciji) završi najudaljeniji od prednjeg gornjeg desnog kuta spremnika (Front-Top-Right).

DFTRC-2 je praktično lokalna pretraga: za svaki objekt provjerava sve dozvoljene rotacije kroz sve EMS-ove i bira najbolju opciju prema kriteriju udaljenosti. U samom pakiranju ipak se koristi rotacija zapisana u kromosomu, pa kromosom i dalje ima značajan utjecaj na cijeli ishod.

Genetski algoritam

Selekcija

Koristio sam elitizam (npr. 5% populacije ostaje netaknuto) i turnirsku selekciju:

• nasumično uzmem 3 jedinke,
• odaberem najbolju,
• ponovim za drugog roditelja.

Križanje

Križanje se pokazalo kao neočekivano osjetljiv dio zbog prirode enkodiranja:

• isti gen u različitim kromosomima može značiti potpuno drugačiji redoslijed nakon sortiranja,
• pa miješanje gena bez konteksta često razbije strukturu.

Zato se SBX i uniformni pristupi nisu pokazali dobrima (slaba stopa učenja; najbolja jedinka se često dobivala praktički slučajno). Najbolje se pokazalo one-point crossover:

• odabere se točka prekida,
• potomci uzimaju lijevi dio od jednog, desni od drugog roditelja,
• potomci zadržavaju blokove strukture i ispadnu sličniji roditeljima.

Mutacija

Mutacija prolazi kroz svaki gen i s malom vjerojatnošću zamijeni vrijednost novom iz [0,1]. Testirao sam više stopa mutacije (1%, 5%, 10%) kako bih našao kompromis između stabilnosti i eksploracije.

Fitness funkcija

Najjednostavniji fitness bi bio samo:

• broj iskorištenih spremnika.

Međutim, ako dva rješenja koriste isti broj spremnika, korisno je dodatno razlikovati kvalitetu pakiranja. Zato se u fitness dodaje i relativno popunjenje najmanje iskorištenog spremnika, npr.:

Fitness = broj spremnika + (najmanje iskorišten volumen / kapacitet spremnika)

To daje finiju gradaciju između rješenja istog broja spremnika. Problem je minimizacijski: cilj je smanjiti fitness.

Analiza rezultata

Kriterij zaustavljanja

Na jednostavnijim instancama optimalno rješenje se pojavilo već nakon nekoliko desetaka generacija, dok se kod složenijih instanci uočava brzo učenje na početku i stagnacija nakon ~100 generacija. Kao praktičan kriterij zaustavljanja koristio sam 100 generacija, a svako mjerenje sam ponovio 20 puta.

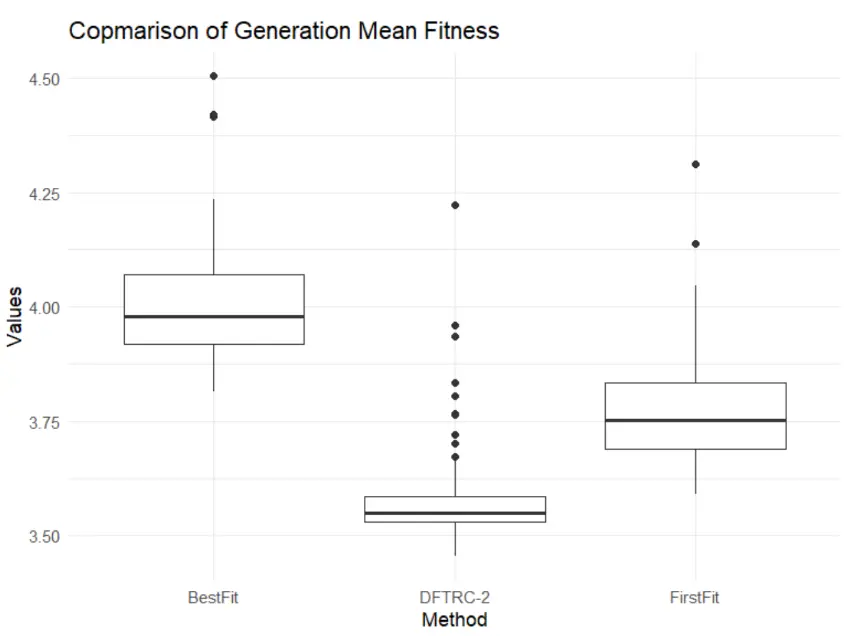
Usporedba heuristika pakiranja

Heuristika pakiranja ima velik utjecaj jer evaluacija gradi cijelo rješenje. U testovima je DFTRC-2 imala jasnu prednost u odnosu na First-Fit i Best-Fit. Zanimljivo, First-Fit se pokazao boljim od Best-Fit, iako bi intuitivno Best-Fit često trebao bolje popunjavati prostor. U praksi to ovisi o dinamici EMS-a i o tome kako izbor manjeg EMS-a utječe na buduće mogućnosti pakiranja.

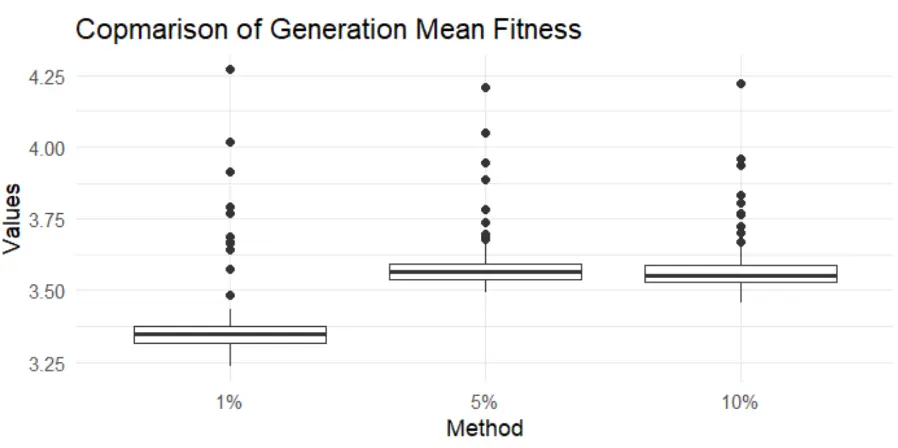
Usporedba stopa mutacije

Testirao sam 1%, 5% i 10% mutacije:

• 1% zna biti odličan ako rano naleti na dobru jedinku, ali često zapne i globalno je ispao najlošiji izbor.
• 10% daje više eksploracije, ali zna razbijati dobre strukture.
• 5% se pokazao najstabilnijim kompromisom i u prosjeku je dao najbolje rezultate.

Zaključak

Trodimenzijsko pakiranje, iako na prvu djeluje trivijalno, u praksi je vrlo zanimljiv i zahtjevan optimizacijski problem koji je aktualan desetljećima. U ovom radu sam implementirao rješenje koje kombinira:

• GA (pretraga prostora rješenja),
• EMS (reprezentacija slobodnog prostora),
• i DFTRC-2 (heuristika izbora prostora).

Analiza je pokazala da:

• operatori križanja poput uniformnog i SBX nisu dobri za ovakav tip enkodiranja,
• one-point crossover čuva kontekst i daje bolju stopu učenja,
• DFTRC-2 dominira nad primitivnijim heuristikama,
• a 5% mutacije je dobar “default” za stabilno napredovanje na složenijim instancama.

Daljnje ideje

• Uvesti dodatna ograničenja (maksimalna težina, zabrane rotacije, lomljivost).
• Probati alternativne reprezentacije kromosoma (npr. direktne permutacije uz specijalizirano križanje).
• Usporediti GA s drugim metaheuristikama (simulirano kaljenje / tabu search) na istim instancama.
• Paralelizirati evaluaciju populacije (evaluacije su često najskuplji dio).

← Natrag Repo →